Improvement Prediction
Introduction
As Roboticists, we are often faced with the “dilemma of optimization”: Should I even optimize, when I have a sub-optimal (heuristic) solution that’s easy to find? This question is especially important when computational resources are scarce, where an optimal solution would take significantly longer to find than a heuristic one.
I was faced with this problem when developing a constrained swarm motion planning methodology, as explained here. In summary, the methodology sought to optimize the motion of the swarm for a multi-task mission through an optimization process that concurrently varied five different decision variables to find their optimal combination. A competing sub-optimal solution was also found. This sub-optimal solution was computationally less intensive than the developed optimal solution. Furthermore, on some problem instances, it even performed nearly as well. I was, thus, compelled to address the “dilemma of optimization”.
To address this problem, I developed and incorporated a decision-making mechanism into the motion planning framework, Figure 1. This mechanism would, first, find the sub-optimal solution for a problem instance at hand. Then, it would use a pre-implementation estimator, as described below, to estimate the improvement in motion performance that can be achieved through the developed optimal planning methodology. Based on this estimate and the available computational resources (quantified through a user-defined threshold), a user could decide if the improvement in performance that the developed optimal planning methodology achieves justifies its additional computational requirements.
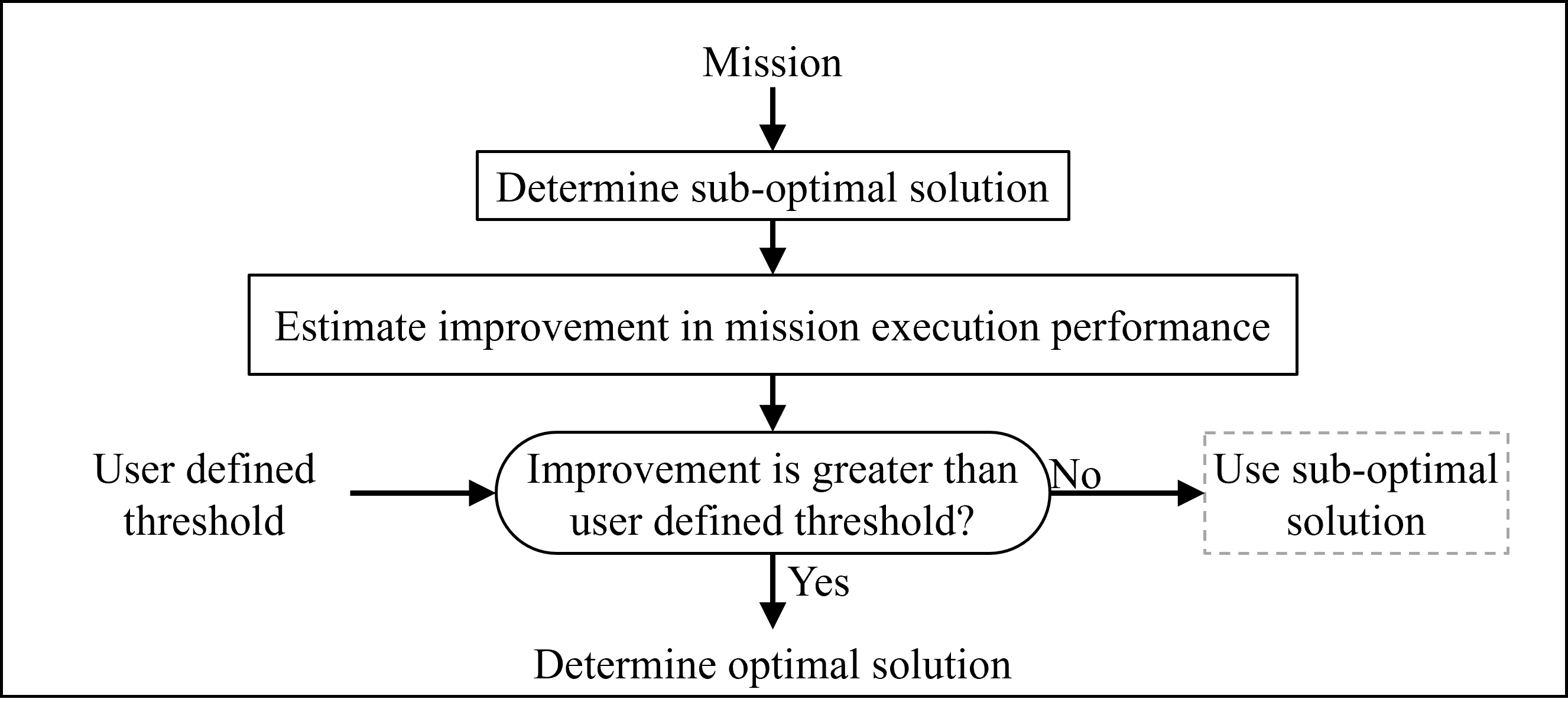
Figure 1: Decision making mechanism.
Pre-Implementation Estimator
A multi-layer perceptron was adopted for estimating the improvement in motion performance that can be achieved by the developed optimal planning methodology compared to its sub-optimal counterpart.
Model Inputs and Architecture
The inputs to the model were selected based on an ablation study, where inputs were systematically removed to evaluate their contribution to the estimation process. The final model considered the following inputs for estimation:
- Swarm- and mission-specific parameters: Number of robots in the swarm, positions of the tasks in the mission at hand, working time of each task, and the number of robots required for the completion of each task.
- The motion plan solution found through the sub-optimal planning methodology: The division of labor. The inputs were concatenated and passed through a single fully connected layer with two thousand neurons, Figure 2.
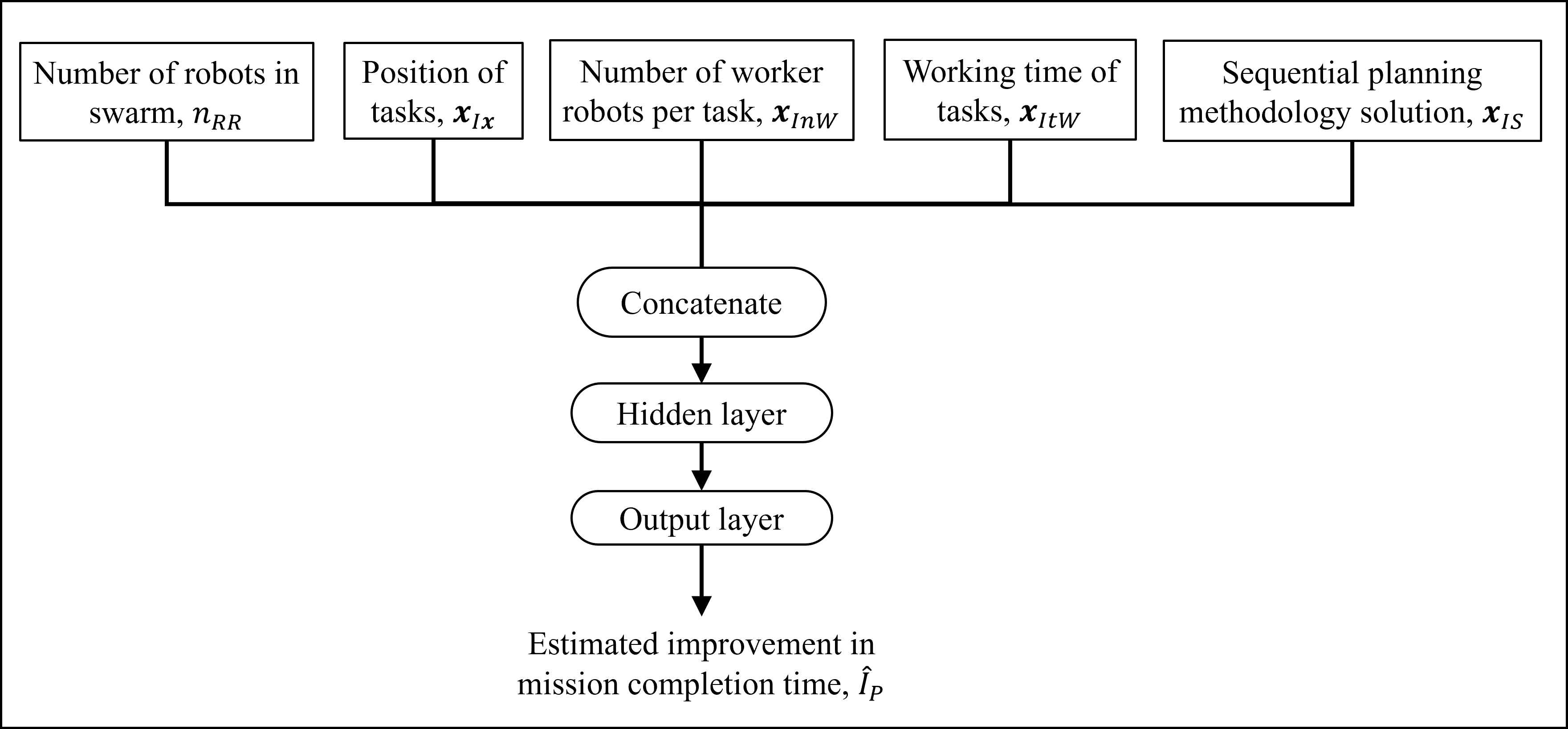
Figure 2: MLP.
Data Collection and Training
The data for this model was generated through a simulation based approach, where ten thousand problem instances (i.e., swarm missions) were randomly generated, and the optimal and sub-optimal solutions for all of them found. The model was, then, trained and validated through a k-fold cross validation procedure.
The developed pre-implementation estimator was able to estimate the improvement in motion performance with an error of approximately 3% of the true value – allowing the user to make well-informed decision on the optimization methodology adopted.
Publication
This work was published in:
K. Eshaghi, G. Nejat, and B. Benhabib, “A concurrent mission-planning methodology for robotic swarms using collaborative motion-control strategies,” J. Int. Rob. Syst., vol. 108, no. 2, pp. 1-26, Apr. 2023.